Define a function that generates Fibonacci series up to n numbers

Define a function that generates Fibonacci series up to n numbers

Note: The Fibonacci numbers are numbers in integer order.
0,1,1, 2,3, 5,8, 13,21, 34,55, 89,144,… … …
In mathematical terms, an order of Fibonacci numbers is defined by the iteration relation.

Learn more:

• Python Fibonacci Series with Example
• What is the Fibonacci series? in java

Fibonacci Series Algorithm:

• Step1. Start
• Step2. read n
• Step3. define Fibonacci function
  • def fibo(n):
• Step4. read x, y
• Step5. check while condition
  • while n>=x:
  • z=x+y
• Step6. End

Fibonacci Series Example:

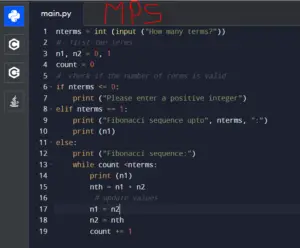
n=int(input("enter the n value:"))
def fibo(n):
    x=0
    y=1
    while n>=x:
        z=x+y
        print(x)
        x=y
        y=z
fibo(n)

Output:

>>>

enter the n value:123
0
1
1
2
3
5
8
13
21
34
55
89
> 

Fibonacci Series code:

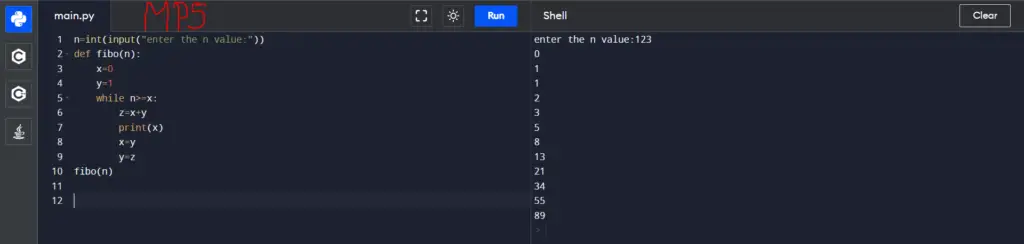
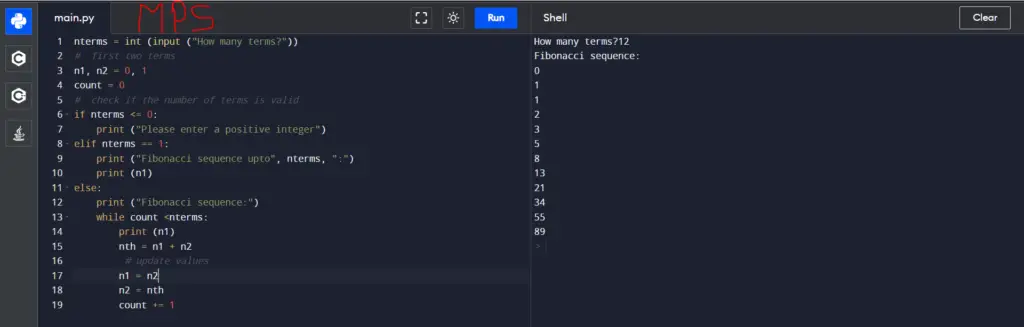
#Program to print the Fibonacci sequence up-to n-th term
nterms=int (input ("How many terms?"))
#first two terms
n1, n2=0, 1
count=0
#check if the number of terms is valid
if nterms<= 0:
    print ("Please enter a positive integer")
elif nterms== 1:
    print ("Fibonacci sequence upto", nterms, ":")
    print (n1)
else:
    print ("Fibonacci sequence:")
    while count<nterms:
        print (n1)
        nth= n1+ n2
         #update values
        n1=n2
        n2=nth
        count+= 1

Output:

How many terms?12
Fibonacci sequence:
0
1
1
2
3
5
8
13
21
34
55
89
> 

Recommended Posts:

• How to Create Forgot System Password with PHP & MySQL
• Datatables Editable Add Delete with Ajax, PHP & MySQL
• Download Login and Registration form in PHP & MySQL
• Export Data to Excel in Php Code
• Hospital Database Management System with PHP MySQL

Get Salesforce Answers