Write a java program that prints all real and imaginary solutions to the quadratic equation

Find the real and imaginary number of the complex number

In this program, we will learn to write a java program that prints all real and imaginary solutions to the quadratic equation ax²+ bx +c = 0. Read in a, b, c, and use the quadratic formula to find real and imaginary numbers calculator.

Algorithm of Real and Imaginary Numbers

According to Linear Algebra of Quadratic Equations, The roots of a quadratic equation aX2+bX+c=0 depends on its discriminant values. The discriminant value is calculated using the formula, d=b2-4ac

• If d=0 then the roots are real and equal and the roots are  -b/4a and –b/4a.
• If d>0 then the roots are real and distinct and the roots are (-b+(b^2 –  4ac)^1/2) / 2a   and    (-b-(b^2 –  4ac)^1/2) / 2a 
• If d < 0 then the roots are imaginary.

Based on these formulas, we are finding the roots of a quadratic equation.

Source Code :

import java.io.*;
import java.util.*;
class Imaginary
{
public static void main(String ar[])
{
int a,b,c,d;
Scanner s=new Scanner(System.in);
System.out.print("The Quadratic Equation is of the form ax2+bx+c=0. \n please enter values \na = ");
a=s.nextInt();
System.out.print("b = "+"\n");
b=s.nextInt();
System.out.print("c= "+"\n");
c=s.nextInt();
System.out.println("The quadratic equation you entered is "+a+"+x2+"+b+"+x+"+c+"=0");
System.out.print("real and imaginary roots are");
d=(b*b)-4*(a*c);
if(d>0)
{
System.out.println("Real and distinct");
double rt1=(-b+Math.sqrt(d))/(2*a);
double rt2=(-b-Math.sqrt(d))/(2*a);
System.out.print("Roots are "+rt1 +" "+rt2);
}
else if(d==0)
{
System.out.println("Real and equal");
double rt1=(-b)/(2*a);
double rt2=(-b)/(2*a);
System.out.print("Roots are "+rt1 +" "+rt2);
}
else if(d<0)
{
System.out.println("Imaginary");
}
}
}

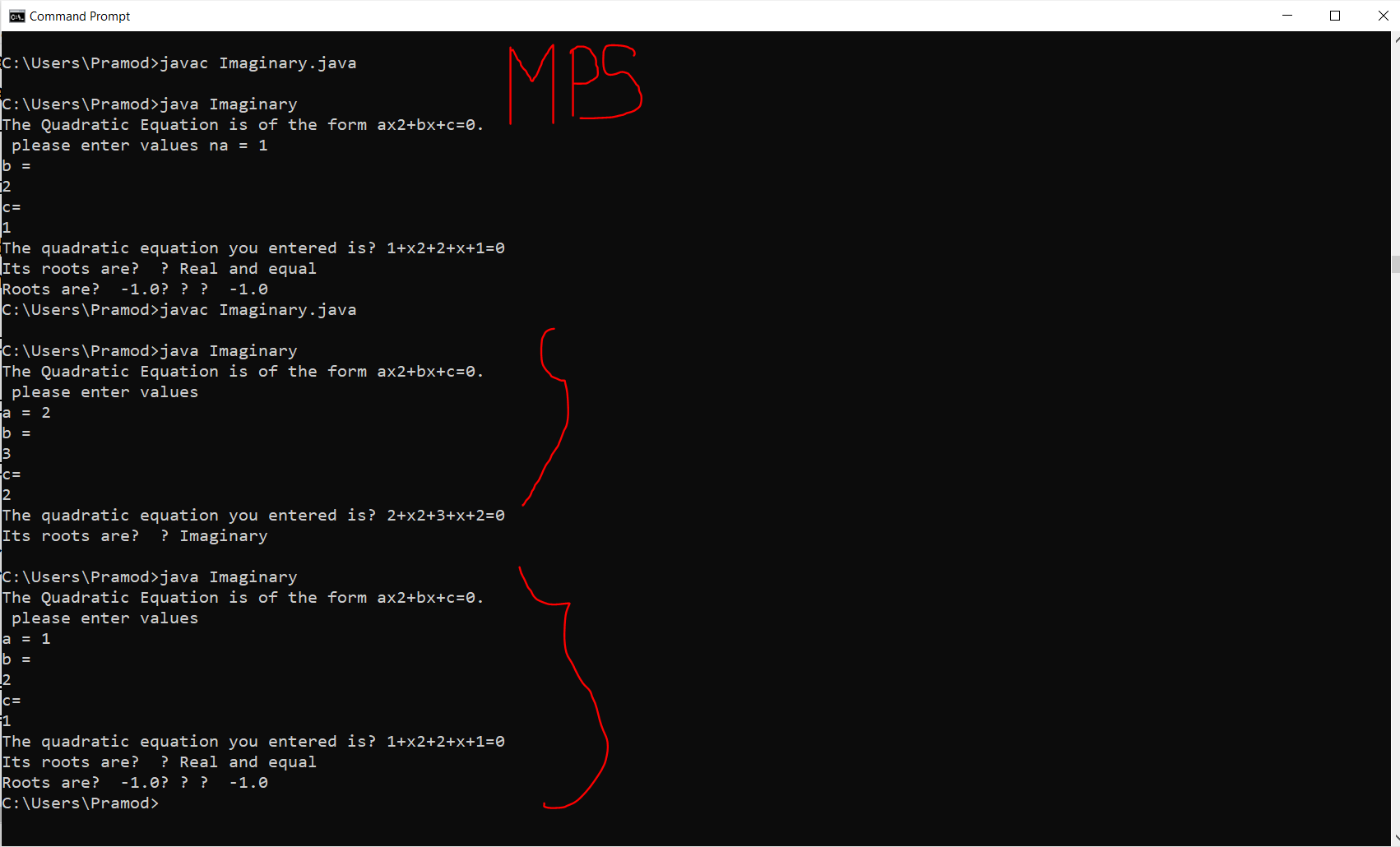
Expected output :